

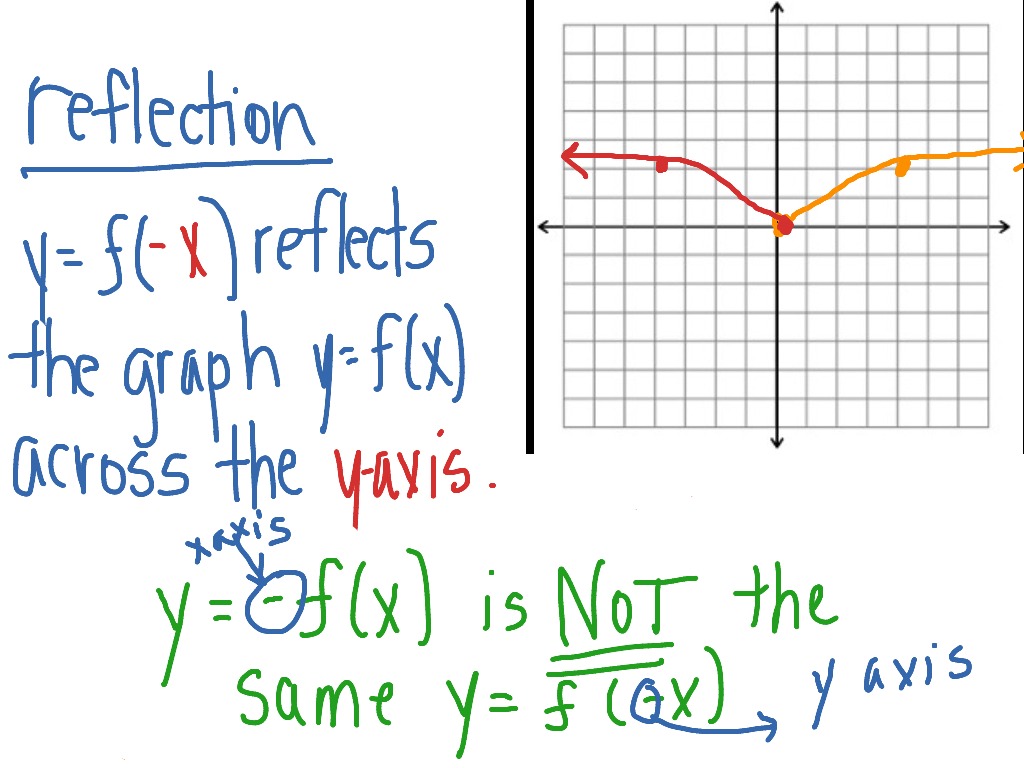
The reflection of the point (x, y) across the line y = x is the point (y, x). When you reflect a point across the line y = -x, the x-coordinate and the y-coordinate change places and are negated (the signs are changed). When you reflect a point across the line y = x, the x-coordinate and the y-coordinate change places. Reflecting over the line y = x or y = -x: (the lines y = x or y = -x as the lines of reflection) The reflection of the point (x, y) across the y-axis is the point (-x, y). When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite. Reflecting over the y-axis: (the y-axis as the line of reflection) Such processes will allow you to see what is happening to the coordinates and help you remember the rule. Or you can measure how far your points are away from the line of reflection to locate your new image. Hint: If you forget the rules for reflections when graphing, simply fold your graph paper along the line of reflection (in this example the x-axis) to see where your new figure will be located. The reflection of the point (x, y) across the x-axis is the point (x, -y). When you reflect a point across the x-axis, the x-coordinate remains the same, but the y-coordinate is transformed into its opposite. Reflecting over the x-axis: (the x-axis as the line of reflection) If P in on the line, then it is its own reflection in line l.

Part II (after the word “and”): The second part of the definition deals with point P being on line ?. The line ? will be the perpendicular bisector of the segment joining point P to point P’. The reflection of point P in this line will be point P’. Part I (up to the word “and”): Here we see line ? and point P not on line ?. Order is reversed.)ĭefinition: A reflection is an isometry where if ? is any line and P is any point not on ?, then r ?(P) = P’ where ? is the perpendicular bisector of \(\overline \) and if P∈? then r ?(P) = P.
distance (lengths of segments are the same).Properties preserved (invariant) under a line reflection: Since naming (lettering) the figure in a reflection requires changing the order of the letters (such as from clockwise to counterclockwise), a reflection is more specifically called a non-direct or opposite isometry. The line of reflection is the perpendicular bisector of the segment joining every point and its image.Ī line reflection creates a figure that is congruent to the original figure and is called an isometry (a transformation that preserves length). Under a reflection, the figure does not change size. A reflection over a line k (notation r k) is a transformation in which each point of the original figure ( pre-image) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line.


 0 kommentar(er)
0 kommentar(er)
